Информатика: Новый полный справочник для подготовки к ЕГЭ - 2018 год
Анализ выигрышных ходов - Теория игр
Конспект
Теория игр — это раздел прикладной математики, посвящённый изучению математических методов поиска оптимальных стратегий в играх. При этом под “играми” понимаются не только собственно игры как соревнования соперников с целью развлечения, но и вообще любые процессы, в которых участвуют две или более сторон, ведущих борьбу за реализацию своих интересов. Каждая из этих сторон имеет свою цель и использует некоторую стратегию, которая может приводить к выигрышу или проигрышу в зависимости от действий соперников. Игра рассматривается как определённый математический объект, который включает игроков, набор стратегий для каждого игрока и выигрыши (“платежи”) игроков для каждой комбинации стратегий. Основные признаки игры как математической модели ситуации следующие:
• несколько участников;
• неопределённость поведения участников, поскольку у каждого из них возможно несколько вариантов действий;
• конфликт интересов участников;
• взаимосвязанность поведения участников, так как результат игры для каждого из них зависит от поведения всех участников;
• правила поведения, известные всем участникам. Методы теории игр находят широкое применение в экономике, политологии, психологии, конфликтологии, биологии (при исследовании поведения животных и теории эволюции), в кибернетике и исследованиях в сфере искусственного интеллекта. Теория игр помогает выбирать наилучшие стратегии с учётом имеющейся информации о других участниках, их ресурсах и возможных действиях.
В теории игр используются две основные формы записи:
• в виде платёжной матрицы (представление игры в нормальной, или стратегической форме);
• в виде ориентированного дерева (представление игры в экстенсивной, или расширенной форме).
Платёжная матрица представляет собой двумерную матрицу, размерность которой определяется количеством возможных стратегий каждого игрока. При этом, например, строки матрицы соответствуют первому игроку, а столбцы — второму игроку. На пересечении строк и столбцов платёжной матрицы записываются выигрыши (положительные числа) и/или потери (отрицательные числа) каждого игрока при выборе им соответствующей стратегии.
Пример нормальной формы игры для двух игроков, у каждого из которых возможно по две стратегии:
|
Игрок 1 |
|||
|
Стратегия 1 |
Стратегия 2 |
||
|
Игрок 2 |
Стратегия 1 |
(1, 0) |
(-1, -1) |
|
Стратегия 2 |
(1, 1) |
(0, 1) |
|
В данной игре использование стратегии 1 обоими игроками даёт выигрыш в 1 очко (условную единицу) игроку 1, не давая выигрыша или проигрыша игроку 2. Использование обоими игроками стратегии 2, наоборот, даёт выигрыш в 1 очко игроку 2, не давая выигрыша или проигрыша игроку 1. Если игрок 1 выбирает стратегию 1, а игрок 2 — стратегию 2, то это обеспечивает выигрыши в 1 очко каждому. Выбор же игроком 1 стратегии 2, а игроком 2 — стратегии 1 невыгоден обоим игрокам (даёт им проигрыш в 1 очко). Анализ такой платёжной матрицы позволяет каждому игроку определить наиболее выгодный для него стиль поведения в игре, избегая явно проигрышных ситуаций и стремясь к выигрышным.
Ориентированное дерево игры представляет собой древовидный граф, корень которого соответствует исходным данным, вершины соответствуют текущим ситуациям в игре, количество ветвей от каждой вершины определяется количеством возможных стратегий каждого играющего, а уровни вершин соответствуют попеременным ходам игроков. Дерево строится до тех пор, пока все его ветви не будут завершены ситуацией, в которой достигнут выигрыш того или иного игрока.
Такой способ представления игры обладает высокой наглядностью, поэтому широко используется в решении задач по теории игр.
Пример фрагмента дерева игры для двух игроков, которые на каждом своём ходе могут выбирать один из трёх вариантов действий (прибавить 1 к исходному числу, вычесть из него 1 или оставить число без изменения; рядом с вершинами надписано текущее значение числа):
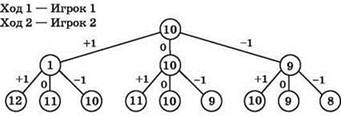
Другая форма представления информации о ходе игры — табличная, она может быть более удобной, если каждый ход может быть реализован большим числом разных вариантов и построение графа затруднено. Например, приведённому выше графу соответствует следующий фрагмент таблицы:
|
Начальная позиция |
Ход 1, игрок 1 |
Ход 2, игрок 2 |
Ход 3, игрок 1 |
|
10 |
11 (“+1”) |
11 (“+1”) |
|
|
10 (“0”) |
|||
|
9 (“-1”) |
|||
|
10 (“0”) |
11 (“+1”) |
||
|
10 (“0”) |
|||
|
9 (“-1”) |
|||
|
9 (“-1”) |
11 (“+1”) |
||
|
10 (“0”) |
|||
|
9 (“-1”) |
Анализ выигрышных ходов производится исходя из того, что оба игрока располагают всей необходимой информацией об игре, способны выполнить грамотный анализ оптимальной стратегии поведения в ней (т.е. “не ошибаются”) и стремятся к выигрышу. Это означает, что при решении задач, связанных с анализом дерева игры, нужно “по очереди играть за каждого игрока”, каждый раз выбирая наиболее выгодный для этого игрока вариант хода. Соответственно, выигрыш или проигрыш того или иного игрока в рассматриваемых в таких задачах играх однозначно зависит только от правил игры и от того, кто из игроков начинает игру (“ходит первым”).
Суть анализа (игрок 1 — это игрок, который делает первый ход начиная игру):
• если в дереве игры имеется хотя бы один путь, который ведёт от корня дерева к концевым вершинам с выигрышем игрока 1, и на этом пути нет никаких выигрышных ходов игрока 2, то при правильной стратегии поведения в данной игре всегда будет выигрывать игрок, делающий первый ход, а указанный путь отмечает выигрышный для него первый ход;
• если в дереве игры для каждого хода игрока 1 встречается хотя бы один путь, ведущий к выигрышу игрока 2, то при правильной стратегии поведения в данной игре всегда будет выигрывать игрок 2, делающий второй ход, а указанный путь отмечает выигрышный для него первый ход.
Если в нескольких ветвях дерева игры получаются одни и те же значения игровых параметров, то можно пронумеровать эти значения параметров и строить для каждого из них отдельное поддерево дальнейшего хода игры.
Графическое изображение дерева игры может быть достаточно громоздким. Можно представить его в виде таблицы, которая строится слева направо; при этом соблюдается договоренность, что верхний, средний и нижний результаты очередного хода всегда соответствуют первой, второй и третьей возможным стратегиям хода игрока.
Разбор типовых задач
Задача 1. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 18 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 35.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 35 или больше камней.
В начальный момент в куче было S камней; 1 ≤ S ≤ 34.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающие ходы.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную стратегию Пети.
Задание 3
Укажите значение S, при котором одновременно выполняются два условия:
у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
Решение
Подобную задачу можно решить, как и предыдущую, путём построения “дерева игры”. Однако существует другой способ решения, который можно назвать “алгебраическим”, — более быстрый и менее громоздкий.
1a. Запишем условия выполнения игрового хода в виде системы неравенств. При этом каждое неравенство соответствует одному из возможных вариантов хода плюс ещё одно неравенство определяет ограничение на возможное количество камней в куче. При этом S в левой части неравенств обозначает количество камней в куче перед первым ходом, а правая часть неравенств указывает условие выигрыша (если в куче станет 35 камней или больше):
• игрок может добавить в кучу один камень: S + 1 ≥ 35;
• игрок может добавить в кучу три камня: S + 3 ≥ 35;
• игрок может увеличить количество камней в два раза: S * 2 ≥ 35;
• в куче изначально может быть не более 34 камней: S ≤ 34.
Решаем полученную систему неравенств, причём учитываем, что поскольку Петя может выбирать любой из трёх возможных вариантов хода, первые три неравенства для хода Пети объединены логической связкой ИЛИ, а последнее, четвёртое неравенство добавляется как обязательное условие (логическая связка И). Нужно также не забывать, что количества камней могут быть только целыми значениями, поэтому получаемые дробные значения нужно округлять в соответствии со знаком неравенства:

Далее объединяем первые три неравенства. Так как они связаны логической связкой ИЛИ, достаточно, чтобы было истинно хотя бы одно из этих условий: ![]()
Решение этой системы неравенств записываем в виде интервала возможных значений S: S ∈ [18 ... 34].
Это и есть ответ на вопрос задания под номером 1а: Петя может выиграть в один ход, если изначально в куче имелось от 18 до 34 камней.
Обоснование ответа: если в куче имеется минимум 18 камней, то Петя своим первым ходом может удвоить количество камней, получить в куче не менее 36 камней и выиграть первым ходом.
1б. Продолжаем решение задачи с помощью системы, но уже не неравенств, а логических условий принадлежности допустимому диапазону значений. Для хода Вани эти условия объединены логической связкой И, так как Ваня должен иметь выигрышный ход при каждом из выбранных Петей вариантов первого хода (И при первом, И при втором, И при третьем). Так же, как и раньше, записывается одно условие для каждого возможного варианта хода. Решение таких условий производится аналогично решению неравенств, только в правой части нужно вычитать соответствующие значения или делить на 2 обе границы интервала, а при получении дробных значений границы — “стягивать” интервал (округлять дробные значения границ до целых внутрь интервала):

Решением такой системы условий является интервал, в который входят только значения S, имеющиеся во всех трёх интервалах. В данном случае три указанных интервала возможных значений 5 пересекаются только в одном значении: S ∈ [17].
Это — ответ на вопрос задания под номером 16: Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом, если изначально в куче имелось 17 камней.
Обоснование ответа: если в куче имелось 17 камней, то после первого хода Пети в куче может стать 18, 20 или 34 камня. В любом из этих случаев Ваня своим первым ходом выигрывает, удвоив количество камней в куче.
2. Продолжаем аналогичным способом запись системы условий. Для хода Пети они объединены условием ИЛИ, так как после первого ответного хода Вани Петя может выбрать любой возможный вариант хода:

Так как в последнем условии единственное предполагаемое значение S оказывается не целым, решением этого условия является пустое множество.
Решением этой системы условий является объединение интервалов: S ∈ [14, 16].
Это ответ на второй вопрос задания: у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: Петя не может выиграть за один ход, но Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня, если изначально в куче было 14 или 16 камней.
Обоснование ответа: в этих случаях Петя не может выиграть первым ходом, так как даже удвоение количества камней в куче даст только 28 или 32 камня. Но Петя может получить кучу из 17 камней, прибавив к 14 камням 3 камня либо прибавив к 16 камням 1 камень. Если теперь в куче 17 камней, то Ваня своим ответным первым ходом даже путём удвоения количества камней не может выиграть (при любом ходе Вани в куче получится не более 34 камней). Но как бы Ваня ни ходил (даже если он увеличит количество камней в куче всего на 1 камень и получит в ней 18 камней), Ваня создаст тем самым для Пети выигрышную ситуацию — Петя выиграет вторым ходом, удвоив количество камней в куче.
3. Составляем систему условий для второго хода Вани.
Прежде всего, рассматриваем отдельно случай, когда Ваня гарантированно выигрывает вторым ходом (первые три условия объединены логической связкой И, так как выигрыш Вани должен обеспечиваться при каждом предыдущем ходе Пети).

Следовательно, у Вани нет возможности гарантированно выиграть вторым ходом.
Теперь рассматриваем возможные условия не гарантированного выигрыша Вани первым или вторым ходом. Отдельно рассматриваются выигрышные условия на первом ИЛИ на втором ходе для первого, второго и третьего возможных вариантов хода (поэтому соответствующие условия в каждом случае объединяются логической связкой ИЛИ). После этого полученные объединения условий выигрыша соединяются в систему логической связкой И, поскольку Ваня должен иметь возможность выигрыша в каждом из показанных трёх случаев. Дополнительно учитываем, что Sне может быть равно значению (значениям), полученному в ответ на вопрос 16, иначе Ваня гарантированно выиграл бы уже своим первым ходом (у нас же в третьем вопросе задания этот случай исключается). В результате вся система условий выигрыша Вани будет иметь вид:

Решение такой сложной системы условий нужно выполнять по шагам:
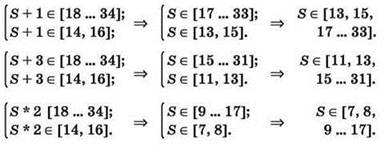
Тогда:
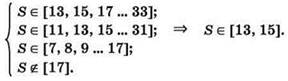
Нужно внимательно отследить пересечение всех указанных интервалов: в результирующий интервал войдут только те значения, которые входят во все три первых интервала, за исключением значения, указанного в четвёртом интервале (17).
Это ответ на вопрос 3 задания: у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом, если изначально в куче было 13 или 15 камней.
Обоснование ответа.
Например, для S = 13 после первого хода Пети в куче будет 14, 16 или 26 камней.
Если после первого хода Пети камней окажется 26, то Ваня своим первым ходом удваивает количество камней в куче и выигрывает.
Если после первого хода Пети камней окажется 14 или 16, то Ваня своим ответным первым ходом прибавляет один камень (для случая 16 камней) или прибавляет 3 камня (для случая 14 камней), чтобы получить в куче 17 камней. Тогда Петя вторым ходом даже при удвоении камней в куче не сможет получить выигрыш. Но при любом втором ходе Пети (даже при прибавлении всего одного камня) камней в куче станет достаточно, чтобы Ваня своим вторым ходом выиграл, удвоив количество камней в куче.
Аналогично обосновывается ответ S = 15. После первого хода Пети в куче будет 16, 18 или 30 камней. Если камней станет 18 или 30, то Ваня уже первым ходом достигнет выигрыша, удвоив количество камней. Если же камней в куче станет 16, то Ваня первым ходом прибавляет 1 камень, получая в куче 17 камней. Далее развитие игровой ситуации такое же, как описанное в предыдущем случае для S = 13.
“Дерево ходов” игры для показанных двух ответов (в ЕГЭ достаточно вычертить “дерево ходов” для одного любого ответа):
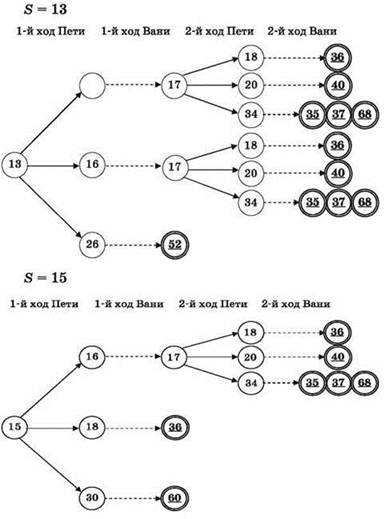
Задача 2. Два игрока, Петя и Ваня, играют в игру. Имеются две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход можно добавить в одну любую кучу один камень или удвоить количество камней в любой куче. Для этого у каждого игрока есть неограниченно много камней.
Игра завершается, когда суммарное количество камней в обеих кучах становится не менее 94. При этом победителем считается тот, кто сделал последний ход, т.е. первым получил выигрышную позицию.
Игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описание стратегии игрока — это описание ходов в любой ситуации, которая может встретиться при различной игре противника.
Задание 1
Для каждой из начальных позиций (9, 42) и (11, 41) укажите, кто из игроков имеет выигрышную стратегию, опишите эту стратегию в каждом случае, объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша.
Задание 2
Для каждой из начальных позиций (9, 41), (10, 41), (11, 40) укажите, кто из игроков имеет выигрышную стратегию, опишите эту стратегию в каждом случае, объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша.
Задание 3
Для начальной позиции (10, 40) укажите, кто из игроков имеет выигрышную стратегию, опишите эту стратегию в каждом случае, объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша. Постройте дерево ходов, возможных при указанной выигрышной стратегии (в виде рисунка или таблицы).
В отличие от предыдущей задачи, где требовалось указать исходное состояние игры, здесь достаточно построить для каждой из представленных начальных позиций “дерево ходов” и проследить в нём выигрышные стратегии на требуемом количестве ходов.
При этом нужно учитывать следующее:
—игроку, который делает ход первым, для выигрыша достаточно получить хотя бы одну выигрышную ситуацию;
—игроку, делающему ход вторым и т.д., для выигрыша требуется получить выигрышную ситуацию при любом предыдущем ходе первого игрока.
Решение
Задание 1
1. Строим дерево ходов для начальной позиции (9, 42). В квадратных скобках указано суммарное количество камней в обеих кучах.
|
Начальная позиция |
1 ход Пети |
1 ход Вани |
|
(9, 42) [51] |
(10, 42) [52] |
(11, 42) [53] |
|
(20, 42) [62] |
||
|
(10, 43) [53] |
||
|
(10, 84) [94] |
||
|
(18, 42) [60] |
(19, 42) [61] |
|
|
(36, 42) [78] |
||
|
(18, 43) [61] |
||
|
(18, 84) [102] |
||
|
(9, 43) [52] |
(10, 43) [53] |
|
|
(18, 43) [61] |
||
|
(9, 44) [53] |
||
|
(9, 86) [95] |
||
|
(9, 84) [93] |
(10, 84) [94] |
|
|
(18, 84) [102] |
||
|
(9, 85) [94] |
||
|
(9,168) [177] |
Таким образом, у Пети (первого игрока) не имеется стратегии, позволяющей достигнуть выигрыша первым ходом. Однако выигрышная стратегия имеется у Вани (второго игрока), который может гарантированно получить своим ответным первым ходом выигрышную ситуацию при любом первом ходе Пети.
2. Строим дерево ходов для начальной позиции (11, 41). В квадратных скобках указано суммарное количество камней в обеих кучах.
|
Начальная позиция |
1 ход Пети |
1 ход Вани |
|
(11, 41) [52] |
(12, 41) [53] |
(13, 41) [54] |
|
(24, 41) [65] |
||
|
(12, 42) [54] |
||
|
(12, 82) [94] |
||
|
(22, 41) [63] |
(23, 41) [64] |
|
|
(44, 41) [85] |
||
|
(22, 42) [64] |
||
|
(22, 82) [104] |
||
|
(11, 42) [53] |
(12, 42) [54] |
|
|
(22, 42) [64] |
||
|
(11, 43) [54] |
||
|
(11, 84) [95] |
||
|
(11, 82) [93] |
(12, 82) [94] |
|
|
(22, 82) [104] |
||
|
(11, 83) [94] |
||
|
(11,164) [175] |
В этом случае также у Пети (первого игрока) не имеется стратегии, позволяющей достигнуть выигрыша первым ходом. Однако выигрышная стратегия имеется у Вани (второго игрока), который может гарантированно получить своим ответным первым ходом выигрышную ситуацию при любом первом ходе Пети.
Задание 2
Строим дерево ходов для начальной позиции (9, 41). В квадратных скобках указано суммарное количество камней в обеих кучах.


При указанной начальной ситуации Петя (первый игрок) может выбрать такой первый ход (прибавить 1 камень ко второй куче, получив ситуацию (9, 42) — в сумме 51 камень), что Ваня (второй игрок) не имеет на своём ответном первом ходе ни одной выигрышной ситуации, но своим вторым ходом Петя может получить выигрыш при любом ответном первом ходе Вани.
Самостоятельно выполните анализ выигрышных стратегий при двух других начальных позициях: (10, 41) и (11, 40).
Задание 3
1. Строим дерево ходов для начальной позиции (10, 40). В квадратных скобках указано суммарное количество камней в обеих кучах.







При указанной начальной ситуации:
— Петя (первый игрок) не может достигнуть выигрыша своим первым ходом;
— Ваня (второй игрок) может получить выигрыш на своём первом ответном ходе, только если первый ход Пети создаёт позицию (20, 40) [60] или (10, 80) [90] (закрасим серым фоном соответствующие ячейки таблицы ходов); остальные варианты первого хода Пети оставляют Ваню без выигрыша на его первом ответном ходе;
— своим вторым ходом Петя может получить выигрыш только при следующих вариантах ответного первого хода Вани (до стрелки указана позиция перед ходом Вани): (11, 40) [51] → (22, 40) [62], (11, 40) [51] → (11, 80) [91], (10, 41) [51] → (20, 41) [61], (10, 41) [51] → (10, 42) [52], (10, 41) [51] → (10, 82) [92] (закрасим соответствующие ячейки серым фоном); в остальных случаях ответного первого хода Вани Петя не может выиграть своим вторым ходом;
— наконец, анализируя оставшуюся незакрашенной часть таблицы, можно сделать вывод, что при указанной начальной позиции (10, 40) [50] и при грамотной игре выигрывает Ваня:
— если первый ход Пети (20, 40) [60] или (10, 80) [90], то Ваня выигрывает ответным первым ходом (см. таблицу выше),
— если первый ход Пети (11, 40) [51] или (10, 41) [51], то Ваня ответным первым ходом может создать такие игровые ситуации ((11, 40) [51] → (11, 41) [52], либо (10, 41) [51] → (11, 41) [52]), что при любом втором ходе Пети у Вани имеется вариант ответного второго хода, приводящий к выигрышу.
Таким образом, при указанных начальных условиях выигрывает Ваня своим первым либо вторым ответным ходом.
Дерево ходов, соответствующих выигрышной стратегии Вани, в графическом виде может выглядеть так:
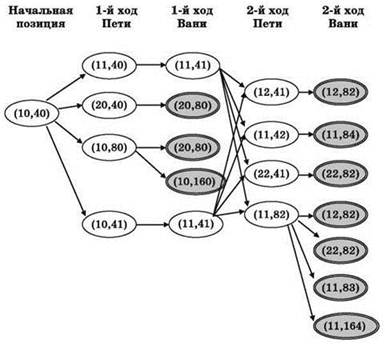
Дерево ходов, соответствующих выигрышной стратегии Вани, также может быть представлено как фрагмент общей таблицы ходов:

